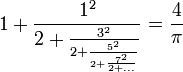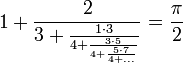::strona główna
:redakcja
:kontakt

::Informacje o PI
:Aproksymacje
:Historia obliczeń
:Kultura PI
:Liczba PI
:Niektóre wzory
:Niewymierność
:Przekształcenia
:Wzory do obliczania
:Znak PI

Wzory do obliczania liczby π

  • Powierzchnia koła jednostkowego:

2\cdot\int\limits_{-1}^{\ 1} \sqrt{1-x^2}\,dx = \pi

  • Obwód okręgu jednostkowego:

\int\limits_{-1}^{\ 1}\frac{dx}{\sqrt{1-x^2}} = \pi

  • François Viète, 1593:

\frac{\sqrt2}2 \cdot \frac{\sqrt{2+\sqrt2}}2 \cdot \frac{\sqrt{2+\sqrt{2+\sqrt2}}}2 \cdot \ldots = \frac2\pi

  • Leibniz:

\sum_{n=0}^{\infty} \frac{(-1)^{n}}{2n+1} = \frac{1}{1} - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \cdots = \frac{\pi}{4}

  • Wallis:

\prod_{n=1}^{\infty} \frac{4n^2}{4n^2-1} = \frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \frac{6}{7} \cdot \frac{8}{7} \cdot \frac{8}{9} \cdots = \frac{\pi}{2}

Powyższe metody są wolno zbieżne. Do szybkich obliczeń komputerowych stosuje się przybliżenie wynikające z tożsamości:

\frac{\pi}{4} = 4 \arctan\frac{1}{5} - \arctan\frac{1}{239}

Funkcję arcus tangens należy rozwinąć w szereg Taylora. Twórcą tej formuły jest angielski matematyk John Machin (1680—1751).

Szybkozbieżnych formuł postaci :\frac{\pi}{4} = \sum_{n}^N a_n \arctan\frac{1}{b_n} pojawiło się więcej, m.in:

  • K. Takano (1982):

\frac{\pi}{4} = 12 \arctan\frac{1}{49} + 32 \arctan\frac{1}{57} - 5 \arctan\frac{1}{239} + 12 \arctan\frac{1}{110443}

  • F. C. W. Störmer (1896):

\frac{\pi}{4} = 44 \arctan\frac{1}{57} + 7 \arctan\frac{1}{239} - 12 \arctan\frac{1}{682} + 24 \arctan\frac{1}{12943}

  • S. Klingenstierna (1730):

\frac{\pi}{4} = 8 \arctan\frac{1}{10} - \arctan\frac{1}{239} - 4 \arctan\frac{1}{515}

Inne metody:

  • Newton:

\frac{\pi}{2}=\sum_{k=0}^\infty\frac{k!}{(2k+1)!!}=1+\frac{1}{3}\left(1+\frac{2}{5}\left(1+\frac{3}{7}\left(1+\frac{4}{9}(1+...)\right)\right)\right)

  • Ramanujan:

\frac{1}{\pi} = \frac{2\sqrt{2}}{9801} \sum^\infty_{k=0} \frac{(4k)!(1103+26390k)}{(k!)^4 396^{4k}}

  • David Chudnovsky i Gregory Chudnovsky:

\frac{1}{\pi} = 12 \sum^\infty_{k=0} \frac{(-1)^k (6k)! (13591409 + 545140134k)}{(3k)!(k!)^3 640320^{3k + 3/2}}

  • Bailey-Borwein-Plouffe Bailey web page (1997)

\sum_{k=0}^\infty\frac{1}{16^k}\left(\frac {4}{8k+1} - \frac {2}{8k+4} - \frac {1}{8k+5} - \frac {1}{8k+6}\right) = \pi

Istnieją także rozwinięcia w ułamki łańcuchowe:

  • W. Brouncker (ok. 1600) [3]

1+\frac{1^2}{2+\frac{3^2}{2+\frac{5^2}{2+\frac{7^2}{2+...}}}}=\frac{4}{\pi}

  • L. Euler (ok. 1755) [3]

1+\frac{2}{3+\frac{1\cdot 3}{4+\frac{3\cdot 5}{4+\frac{5\cdot 7}{4+...}}}}=\frac{\pi}{2}
Nadaj zmiennej a wartość 3
Nadaj zmiennej b wartość 3
Nadaj zmiennej s wartość sqrt(3)/2 (Sinus kata Pi/a)
Nadaj zmiennej t wartość sqrt(3) (Tangens kąta Pi/b)
Dopóki wartość bezwzględna z różnicy s i t jest większa od zadanej dokładności to
Nadaj zmiennej a jej podwojona wartość
Nadaj zmiennej b jej podwojona wartość
Nadaj zmiennej s wartość sinusa połówkowego
Nadaj zmiennej t wartość tangensa połówkowego

Pi leży w przedziale [as;bt]
Wszelkie Prawa Zastrzeżone! Design by White DragoN .