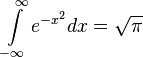::strona główna
:redakcja
:kontakt

::Informacje o PI
:Aproksymacje
:Historia obliczeń
:Kultura PI
:Liczba PI
:Niektóre wzory
:Niewymierność
:Przekształcenia
:Wzory do obliczania
:Znak PI

Niektóre wzory zawierające

Geometria

  • 2\pi r\quad - obwód okręgu o promieniu r

  • S=ab\pi\quad - pole elipsy o półosiach równych a i b

  • V_n=\frac {\pi^\frac{n} {2} \ } {\Gamma(\frac{n} {2}\ +1)}\ r^{n} - objętość n wymiarowej kuli o promieniu r

  • 4\pi r^{2}\quad - powierzchnia kuli o promieniu r

  • Miara łukowa kąta półpełnego równa jest π radianów

  • V = πr2H - objętość walca

Analiza matematyczna

  • \zeta(2) = \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \cdots = \frac{\pi^2}{6} (Euler)

  • \zeta(4)=\frac{\pi^4}{90}

  • \int\limits_{-\infty}^{\ \infty} e^{-x^2} dx = \sqrt{\pi} (rozkład normalny)

  • n! \approx \sqrt{2 \pi n} \left(\frac{n}{e}\right)^n (wzór Stirlinga)

  • e^{\pi i} + 1 = 0\; (Wzór Eulera, nazywany również najpiękniejszym wzorem matematyki)

  • \pi = 4 \int\limits_{0}^{\ 1} \frac{1}{1+x^2};

Teoria liczb

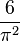  • Prawdopodobieństwo tego, że dwie losowo wybrane liczby całkowite są liczbami względnie pierwszymi wynosi \frac{6}{\pi^{2}}.

  • Średnia liczba sposobów na zapisanie liczby naturalnej jako sumy dwóch liczb całkowitych, których pierwiastek też jest liczbą całkowitą, wynosi \frac{\pi}{4}.

W powyższych przypadkach prawdopodobieństwo i średnią rozpatruje się w sensie granicznym np: rozważamy prawdopodobieństwo dla zbioru liczb {1, 2, 3,…, N} a następnie obliczamy granicę przy N dążącym do nieskończoności.
Wszelkie Prawa Zastrzeżone! Design by White DragoN .